Does P=NP?
What do these 6 pictures have in common?






Definitions
Proof
1) Sub-set problems can have multiple viable solutions. 2) Viable solutions to sub-set problems can exist on independent dimensions. 3) Since viable solutions to sub-set problems can exist on independent dimensions, at least one solution must be calculated per dimension per sub-set problem. 4) If at least one solution must be calculated to sub-set problems per dimension, NP problems with multiple dimensions cannot be solved in polynomial time. 5) Since a characteristic of all P problems is that they can be solved in polynomial time, P ≠ NP.
What is P? what is NP?
P is what we call a certain type of problem. This type of problem has two characteristics: 1) The problem can be quickly solved, through series of arithmetic steps and true or false statements. Like 10 + 10 + 10 = ? 2) The solution can be quickly verified, through series of arithmetic steps and true or false statements. Like “Is 30 the sum of 10 + 10 + 10?” NP is what we call a certain type of problem that has at least one of those characteristics. Specifically,: 2) The solution can be quickly verified, through series of arithmetic steps and true or false statements. Like looking at a finished Sudoku, or seeing the colors matching on all side of completed Rubix cube The question is: Are P and NP the same type of problem? Since you can easily verify a solution to an NP problems, does that not also mean you can easily find the solution? Does characteristic #2 imply characteristic #1? Does P = NP?Why does the P vs. NP problem exist?
I believe that the P vs. NP question arises as a thought experiment because people, myself included, tend to think about solving NP problems in terms of a decision tree. Like branches. Or nodes.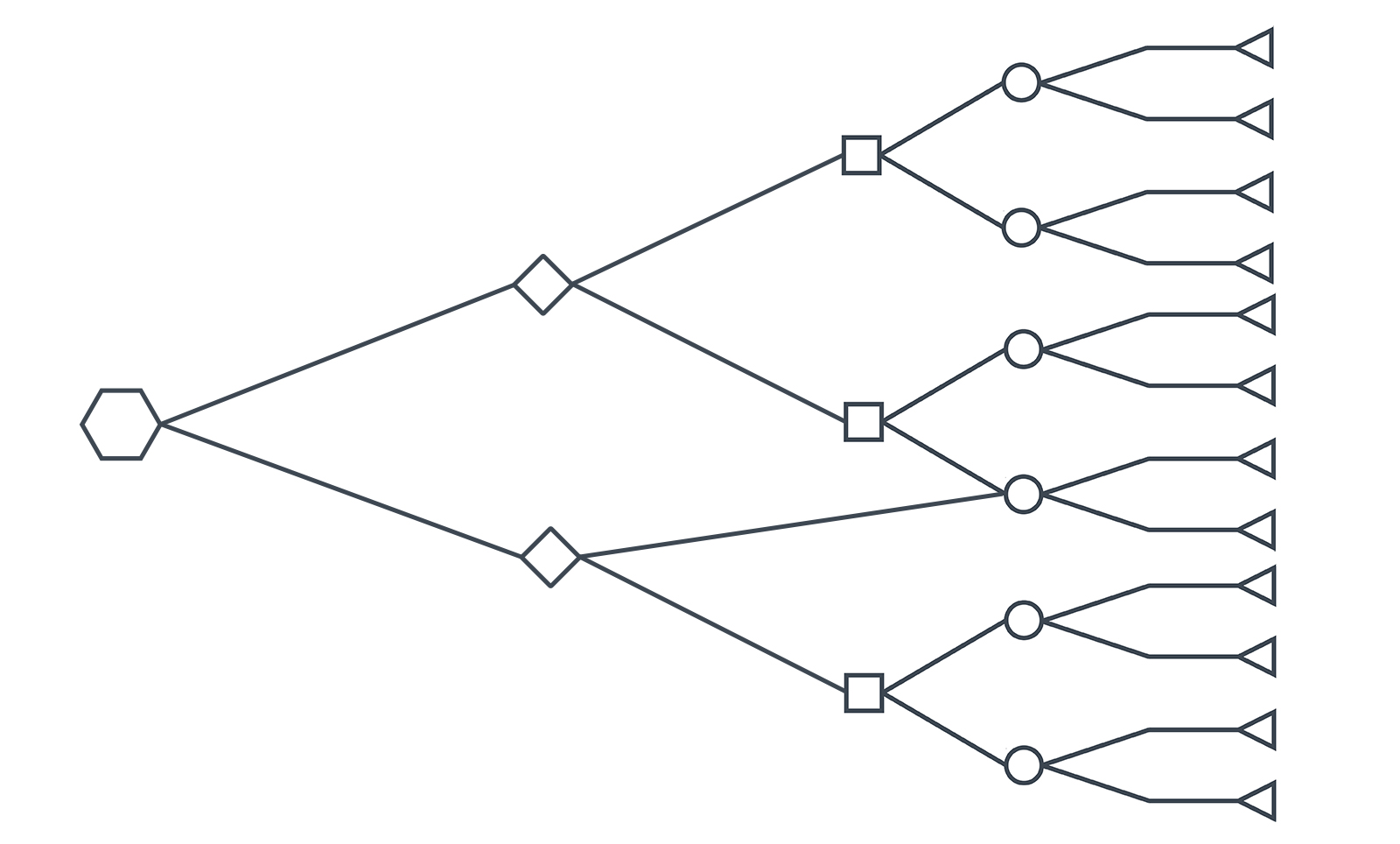
Why do we think in terms of decision trees?
We think about NP problems in terms of the shape of decision trees because that is accurately how the NP problems are computed. They test every option. They go down a path to conclusion, then “back up”, then try a small variation of that path. Then back up more. Then try a new path. And so on. This trial and error approach is called a ‘brute force’ method. It’s a lot like trying to guess a 4 digit numerical password. You have to trial and error each variation, like this: 1111 1112 1113 1114 … 9998 9999The problem is:
It’s very attractive to imagine that if a solution can be easily verified, the path to that solution can also be easily deconstructed.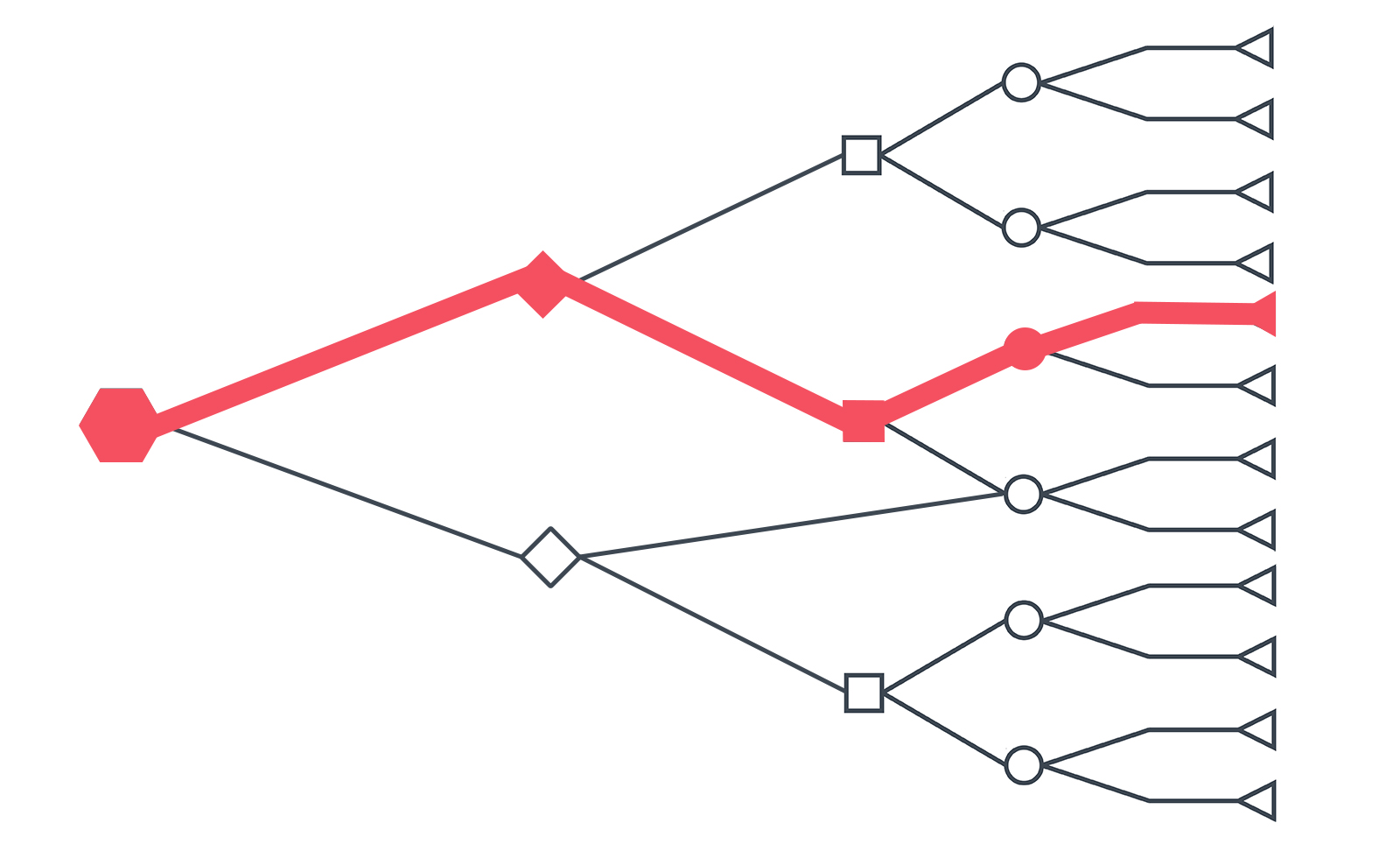
Why is there not a deterministic way of approaching NP problem?
It’s hard to make a case against determinism in the real world. We understand that adding 2 to 2 creates 4. We understand in physics that matter and forces interact with each other in predictable manners. So because the future is, in this way, predictable, it’s attractive to think that an outcome can always be reverse engineered. But below we’ll explore why that can’t always be. The problem is that not all outputs have just one possible input. When we ask “What is 10 + 8”, we understand the answer is 18. There is roughly speaking a 1 for 1 computational input and output. But if we are asked “What are two numbers that add together to get 18?”, there are more than one answer. 9+9=18 8+10=18 7+11=18 … 2+16=18 1+17=18 In this case, we have a 1 to 9 input to output. There are 9 equally valid answers to this problem. NP problems can be thought of as problems that have multiple solutions, and that can be nested within other problems with multiple solutions. Our folly is believing that when an NP problem has only one solution, it must have been determined. Again, a decision tree is attractive because you think ‘determinism’. But. To verify a solution is correct is NOT to verify only one solution exists.Okay, how should we model NP problems?
The first thing to understand is that computing NP problems is an optimization problem. Woah. In fact, an NP problem can be thought of an optimization problem where infinitely more data makes the answer more confident, but because of “constraints” (explained below), there may be only one solution. Let me explain…NP is an optimization problem, not an arithmetic one
What is an ‘arithmetic’ problem?
One unique characteristic of an arithmetic problem is that you don’t need to have all information to solve the next “step”. If a problem is a combination of many sub-problems, the answer to the first problem you solve does not depend on answers to future steps. You don’t have to review the solutions to other sub-set problems to find the solution the current one. What does that mean? Imagine adding two large number together. But imagine that not all information about the problem is “accessible” at the onset. Like this…
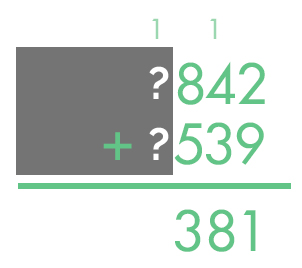
 We begin to add together two four-digit numbers while having some parts of the equation hidden.
We begin to add together two four-digit numbers while having some parts of the equation hidden.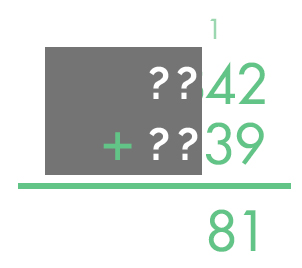
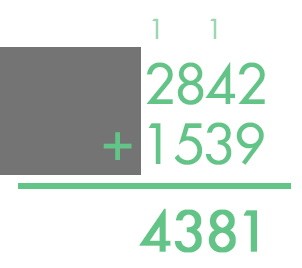
NP Problems are an optimization problem. More data = more confidence.
The reason NP problems are so costly is because of the time required for computing is so high. As a ‘decision tree’ model gets larger, with more branches, there are exponentially more unique paths to trial and eliminate (like trying to guess a password by guessing every variation). Unlike arithmetic problems, the time required for computing is quite literally the time required for reviewing all possible data (all branches) and eliminating options. Because knowing a solution to a problem does not mean you know it’s the only solution, computing time is spent doing the following: discovering more solutions and eliminating non-solutions. It’s the discovery process that eats up so much computing time in a non-polynomial way (ie. having to check all branches). Okay. So how do we begin to conceptually model this?Introducing: Venn Diagrams

NP Problem #1: What do these photos have in common?






Sub-set Problems
Well, first you need to understand that the NP problem “What is common between these 6 photos?” is made up of a sub-set problem: “What is in this photo?” The sub-set question, “What is in this photo?”, must be solved 6 times. That is, one time for each photo.Sub-solutions
Secondly, you would begin sub-dividing each element in a photo into individual things (sky, clouds, plants, road, cars, people, animals, etc.). Let’s call the total number of sub-solutions “n”. In these 6 photos, we have a nearly infinite “n”. Sub-solutions (n) are the total number of answers to the sub-set question: “What is in this photo?” Some of these n’s correlate with each other. For example, the existence of a car in each photo correlates to the existence of wheels.Dimensions
But thirdly, we have to ask ourselves if we are just looking for common things in the photo. For example, do we need to check if the photos have a common height? Width? Aspect ratio? Is it possible that each photograph was taken by the same photographer? Were they all taken at the same time? Aren’t they all being displayed on your monitor screen? There are things that these photos can have in common outside of what is technically in the photo. You’ll quickly realize that there are multiple dimensions you could be measuring each photo against. These dimensions don’t necessarily correlate with each other. They are what’s called statistically independent. In the same way that knowing the height of a given shape doesn’t tell you any information about that shapes width, answers to sub-set problems across independent dimensions can not exclude the existence of each other. If we’re told that red is viable solution to the question “What color can we paint our firetruck?”, that does not exclude the possibility that firetrucks can be painted other colors. In this example, each color is on an independent dimension. Let’s call the number of dimensions a problem has “d”. In these 6 photos, we have nearly infinite “d”.Finding a solution
Okay. So the total number of sub-solutions (n) for each dimension (d) give us the total number of things to check for in each photo. n1 + n2 + n3 + n4 + … + nd or this can also be written as: Once identified, we would need to verify each n exists in every photo. So that means we perform one true or false statement per photo per element. To compare only two photos, for example, it would look like this:
Once identified, we would need to verify each n exists in every photo. So that means we perform one true or false statement per photo per element. To compare only two photos, for example, it would look like this:
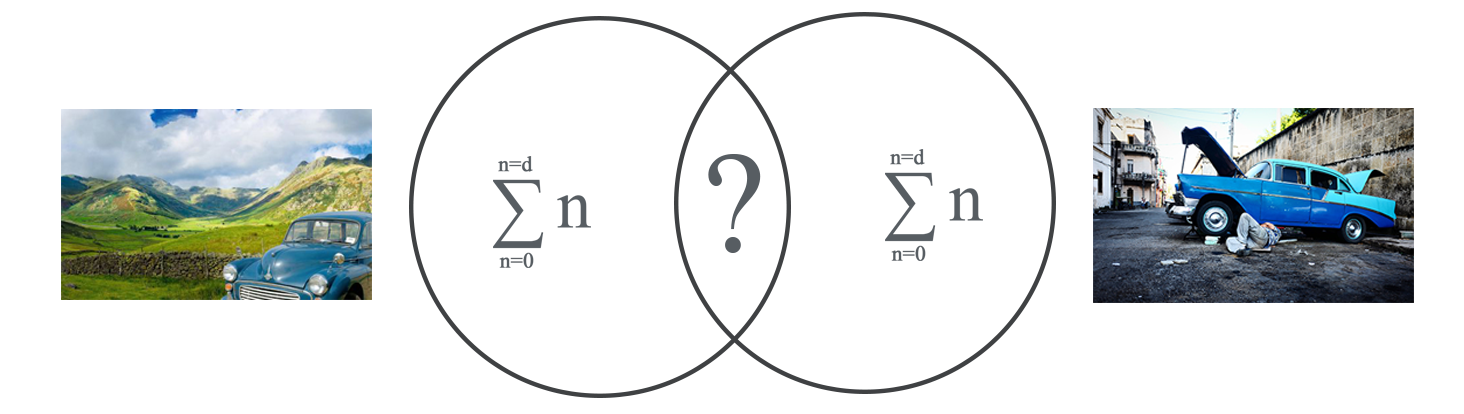

Let’s simplify the problem even more…
Okay, so what if we simplified the pictures? And what if we added a constraint to the question? For example, “What shapes do the below pictures have in common?” In this case, let’s only deal with one dimension, shapes within the photo. So now d=1. So what shapes do these three pictures have in common?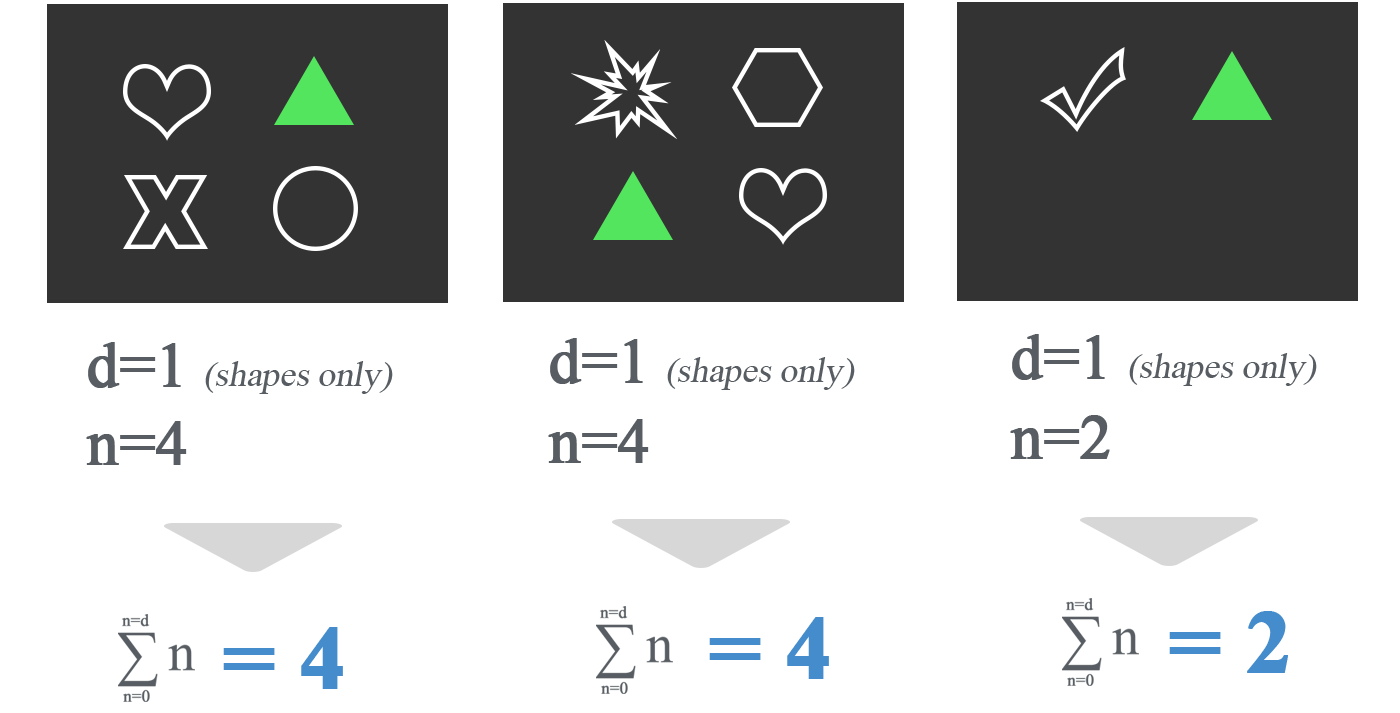
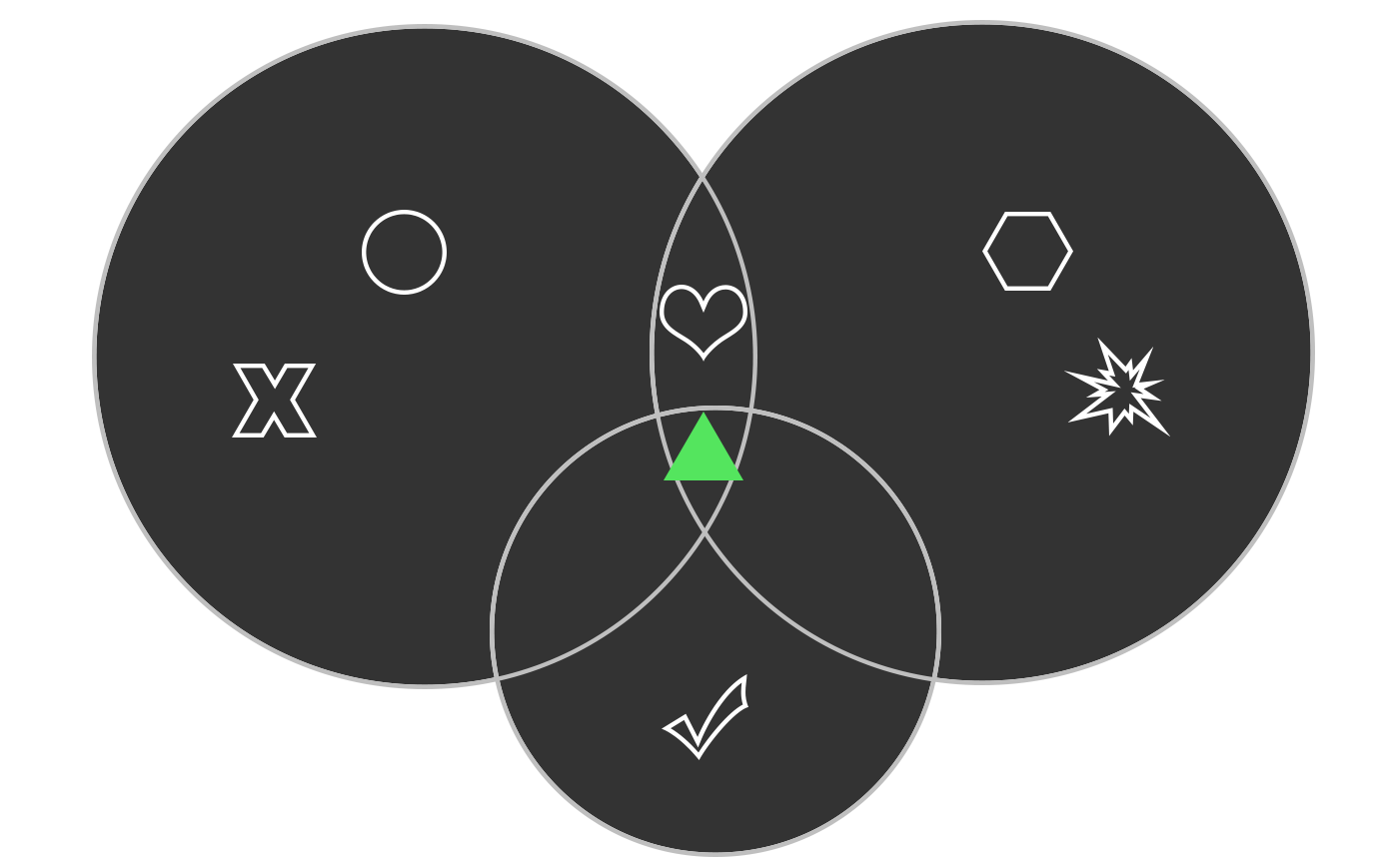
Conclusion
Because NP problems (like “What shapes are common between these pictures?”) are comprised of sub-set problems with multiple answers (like “What shapes are in this picture?”), all answers to sub-set problems must be calculated before finding an answer. Even if there is only one final solution (ie. triangle), since sub-set problems have multiple equally valid solutions, the solution cannot be found in polynomial time.NP Problem #2: What is the answer to this riddle?
 Okay, so first, let’s model this question conceptually using a Venn Diagram.
Okay, so first, let’s model this question conceptually using a Venn Diagram.
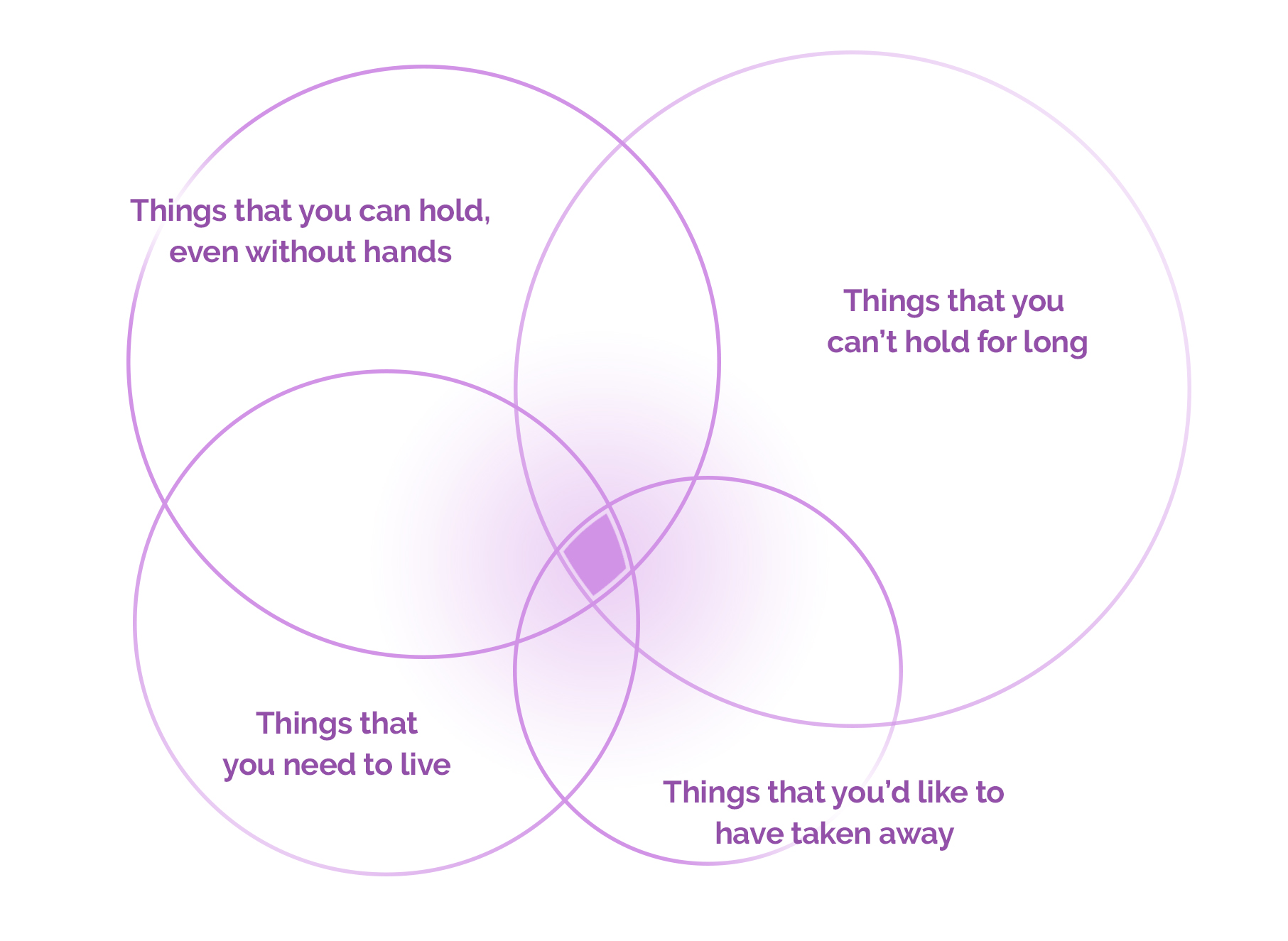 Already, we are seeing that sub-set questions have multiple answers:
What can be held, even without hands? stocks, a purse, a basket on your head, a thought, someone in contempt of court…
What can’t be held for long? a heavy weight, an ornery cat…
What are things that you need to live? air, food, deoxyribonucleic acid…
What, when taken away, is good? pain, suffering, an empty plate…
Already, we are seeing that sub-set questions have multiple answers:
What can be held, even without hands? stocks, a purse, a basket on your head, a thought, someone in contempt of court…
What can’t be held for long? a heavy weight, an ornery cat…
What are things that you need to live? air, food, deoxyribonucleic acid…
What, when taken away, is good? pain, suffering, an empty plate…
Conclusion
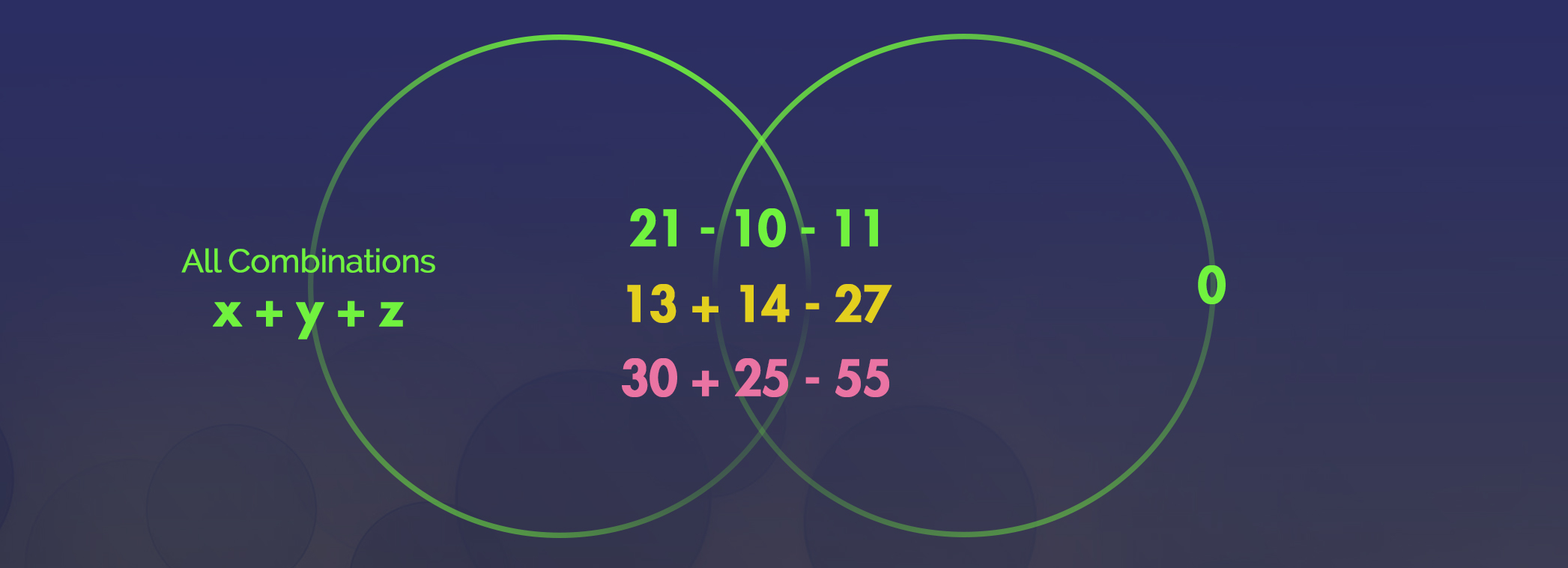
Again, even though we only have 4 sub-set questions, we quickly see that each sub-set question has as many calculations as there are concepts or words in the dictionary. We would get to the B section in the dictionary before we got to your breath. A viable solution. But is breath the only correct answer? Or even the optimal one? This is another illustration of how the sheer number of solutions to subset problems and the independence of sub-set problems prevent NP problems from being solved in polynomial time. You can never be sure an NP problem doesn’t have more solutions until you’ve exhausted/eliminated all other options.NP Problem #3: What are three numbers from this list who’s sum equals 0?

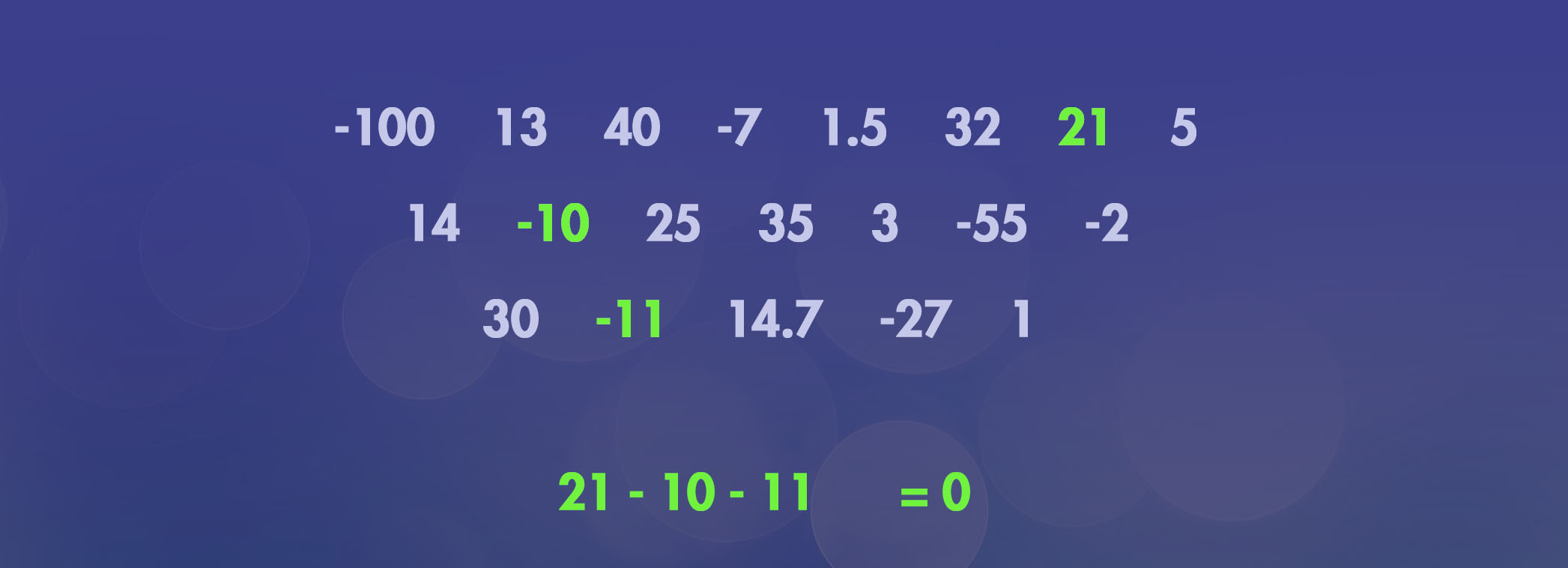
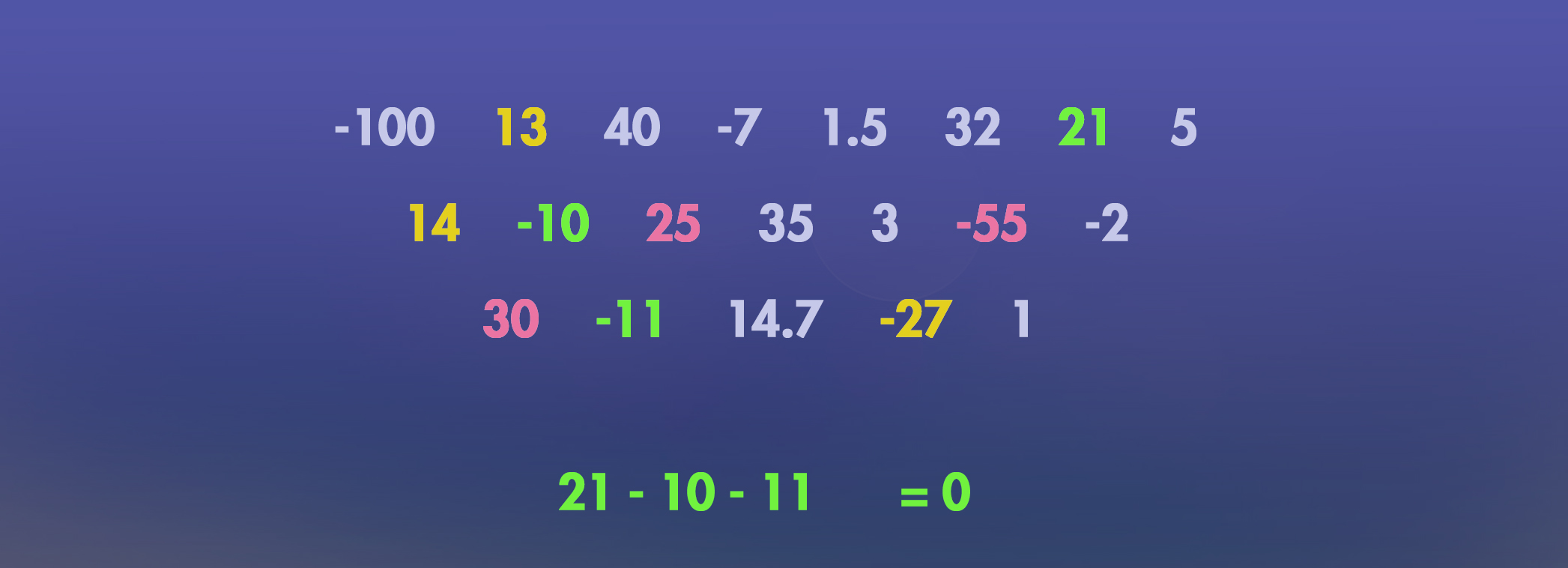
Constraints: Decreasing the computing time of NP problems
The nature of the constraints of this NP problem, that three numbers must total 0, demands that no two negative numbers can total more than the largest positive number. And that no two combinations of positive numbers can total more than the most negative number. While discovering totals for combinations of two numbers in our example, we at some point discover that the sum of the two most negative numbers is -155 (-100 and -55). This means that no positive number can be greater than 155. This is a great insight! We also discover that the sum of the two largest numbers is 75 (40 + 35). This means that no negative numbers less than -75 can be in the answer. This actually rules out “100” as a possible answer choice. Look at that! We developed a logical constraints to eliminate 100 as an option. This means that we no longer have to compute all combinations of the sub-set problem 100 + y + z. This saves us time! Conceptually, this can be thought of as a circle in the Venn Diagram getting smaller. The circle now contains less calculations to check as it can now rule out “100” as being part of the solution. But we can’t reduce any further. -55 is the next most negative number. But 30 and 40 together sum more than the absolute value of -55.What are “Constraints”?
What is a constraint?
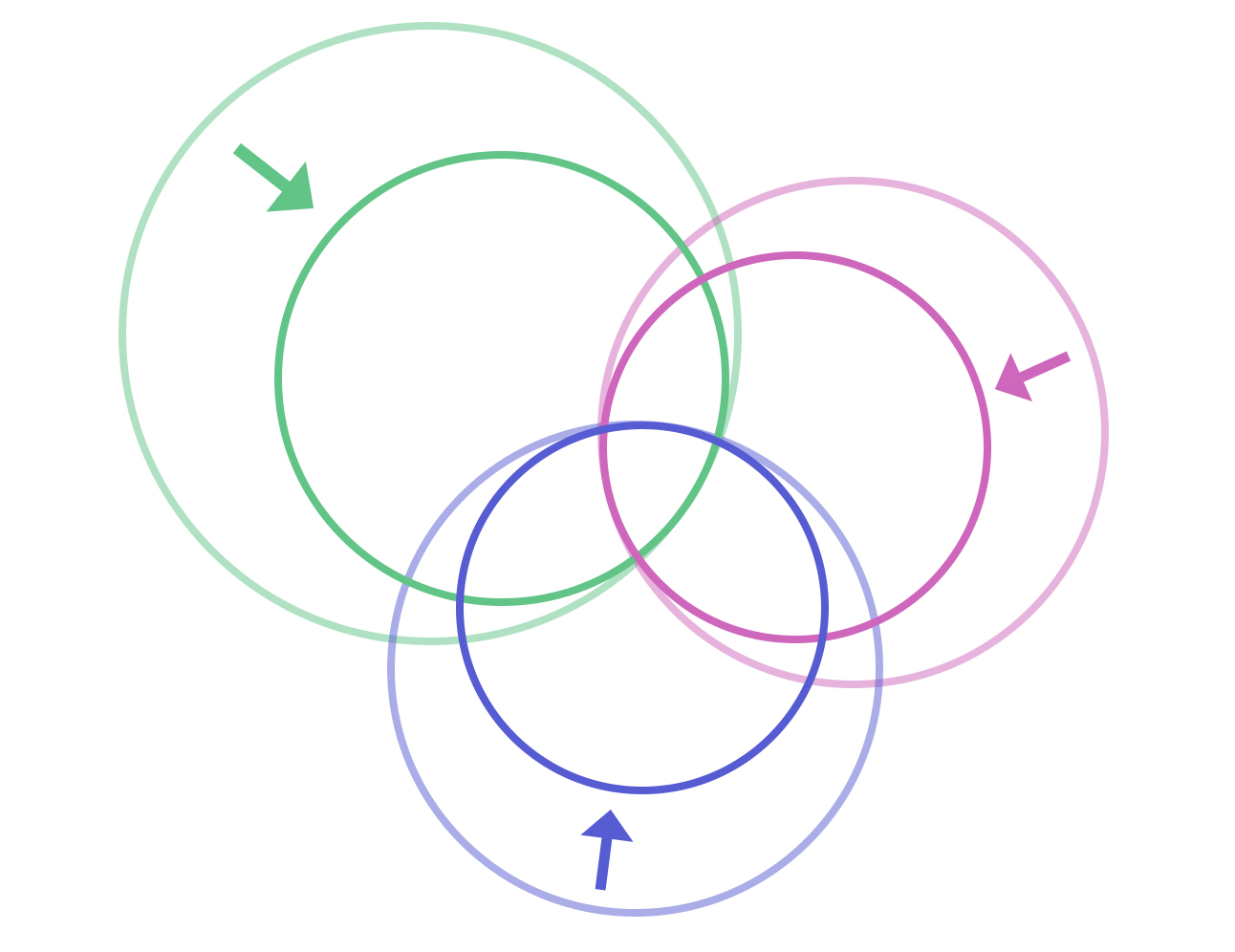 A constraint is anything that reduces the number of dimensions (d) or sub-set problem solutions (n). Constraints reduce the size (area) of a Venn Diagram circle.
Consider this.
For the problem: “What’s a large number you can think of?”, you might think to answer 100 or 2,859.7 or 408,395, or 9,999,9999….
But for the problem: “What’s the largest integer you can think of between 200 and 500?” the solution would be 499.
This is an example of how constraints added to questions can give you a single solution where before multiple solutions may have existed.
A constraint is anything that reduces the number of dimensions (d) or sub-set problem solutions (n). Constraints reduce the size (area) of a Venn Diagram circle.
Consider this.
For the problem: “What’s a large number you can think of?”, you might think to answer 100 or 2,859.7 or 408,395, or 9,999,9999….
But for the problem: “What’s the largest integer you can think of between 200 and 500?” the solution would be 499.
This is an example of how constraints added to questions can give you a single solution where before multiple solutions may have existed.
How can constraints help us solve NP problems more quickly?
The above problem is an example of how constraints can turn an NP problem into a P problem. 1) We know that intergers are multiples of 1 for whole numbers 2) We know that the smallest whole number ≥ 500 = 500 Therefore, 500 – 1 = 499. This problem can be calculated and verified in polynomial time, regardless of the inputs. We could change 200 to 50 and change 500 to 781.2, and still solve this problem in polynomial time: 781. Constraints can make an NP problem a P problem, but the existence of independent dimensions (see example #1) is proof that not all NP problems can be P problems.Understanding Constraints: Mario, Battleship, & Sudoku
Ultimately, NP problems are just optimization problems with constraints. Super Mario: Base Question: “What path can be taken from point A to point B?” Number of Viable Solutions: Infinite Optimal Answer: A straight line Constraints: Obstacles, time limit Optimal Answer with Constraints: If an obstacle is blocking a straight line, more than one path can be optimal Sudoku: Base Question: “Can you place numbers 1-9 in an 9×9 grid so that no numbers are duplicated across any row, any column, or within nine 3×3 grids?” Number of Viable Solutions: 6,670,903,752,021,072,936,960 Optimal Answer: Any of 6,670,903,752,021,072,936,960 viable solutions are equally valid Constraints: Some numbers are pre-filled in Optimal Answer with Constraints: Most Sudoku’s have enough constraints (pre-filled numbers) that only 1 final solution exists. But being given a final solution does not necessarily mean it’s the only one. Battleship Base Question: “Where are 17 unknown points on a 10×10 grid?” Number of Viable solutions: 1 Optimal Answer: Wherever the 17 points are on the 100 point grid Constraints: The 17 points will be grouped into five straight lines of different lengths: 5 points (Aircraft Carrier), 4 points (u Boat), 3 points (Submarine), 3 points (Cruiser), and 2 points (Destroyer) Optimal Answer with Constraints: There is still just 1 viable solution, but the constraints allow you to find a solution in less time because of the adjacent nature of points being grouped together.Reducing n : An approach to solving NP problems more quickly
Understanding the nature of constraints will allow us to solve NP problems more quickly, but on a case-by-case basis. While some constraints allow us to prioritize brute force method (ie. targeting adjacent points near a ‘hit’ in Battleship), other constraints reduce the number of n‘s that need to be calculated (ie. how we eliminated 100 as being part of a viable solution in our example #3). Using this model of thinking, we should conceptually imagine attacking NP problems as reducing the size (area) of the circles in a Venn Diagram.
By reducing the size of these overlapping circles, we can reduce the computing time necessary to find all solutions to a given NP problem.
While some NP problems can be solved in polymonial time (like an algorithm to solve a Rubix cube), remember that having a polynomial solution does not mean it’s the optimal solution. There will always a cost of discovery–this is the nature of having independent dimensions. But we can continue to build faster and stronger computers to brute force through decision trees, and we can optimize these computing efforts by understanding constraints & inputting rules that eliminate or prioritize branches of the decision trees.
Using this model of thinking, we should conceptually imagine attacking NP problems as reducing the size (area) of the circles in a Venn Diagram.
By reducing the size of these overlapping circles, we can reduce the computing time necessary to find all solutions to a given NP problem.
While some NP problems can be solved in polymonial time (like an algorithm to solve a Rubix cube), remember that having a polynomial solution does not mean it’s the optimal solution. There will always a cost of discovery–this is the nature of having independent dimensions. But we can continue to build faster and stronger computers to brute force through decision trees, and we can optimize these computing efforts by understanding constraints & inputting rules that eliminate or prioritize branches of the decision trees.